| Autore |
Discussione |
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
 Inserito il - 16 gennaio 2013 : 15:31:35
|
Ragazzi mi aiutate a capire come risolvere questi due esercizi?
Problema 1: Corea di Huntington
Immagine:
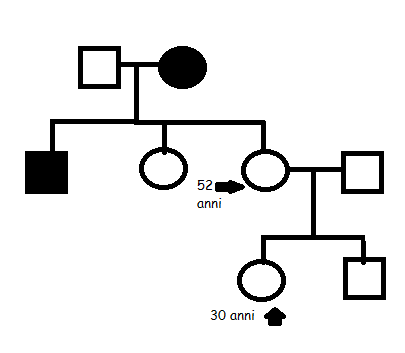
7,08 KB
Vuole sapere qual è la probabilità di II,3 di aver ereditato l'allele malato? E qual è la probabilità di III,1 di aver ereditato l'allele malato?
a 52 anni = penetranza 55%
a 30 anni = penetranza 10%
Io ho ragionato così:ho utilizzato Bayes
II,3 Portatore Non portatore
P a priori 1/2 - 1/2
P condizionale 0,45 - 1
P congiunta 0,225 - 0,50
P finale 0,31 - 0,69
Ora intuisco che devo fare la stessa cosa per III,1 aggiungendo però la probabilità della mamma!ma come faccio da un punto di vista matematico?Non so quali calcoli fare!!
Problema 2:Fibrosi Cistica
Immagine:
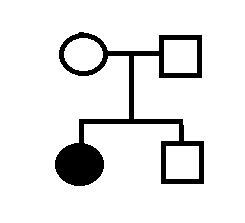
3,37 KB
II,2 risulta essere positivo al test per la fibrosi cistica.
La sensibilità del test è del 90%
La specificità è dell'85%
Quale probabilità ha di non essere portatore?
Qui invece non so proprio come muovermi...non so se calcolarlo con Bayes oppure no! Spero che qualcuno mi aiuti! Grazie!
|
|
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 16 gennaio 2013 : 18:01:28
|
ESERCIZIO 1:
ok per la prima parte.
Poi, senza considerare per un attimo la penetranza per III-1, una volta che hai stabilito la P che la madre sia portatrice come calcoleresti la P che la figlia abbia ereditato l'allele?
Quella sarà la tua probabilità "a priori" da inserire nel test.
N.B. se questa ultima probabilità la calcoli senza usare bayes (mettendo però la penentranza) in realtà il risultato è molto simile a quello che ottieni con bayes.
ESERCIZIO 2:
vediamo se questi aiuti ti servono per impostare l'esercizio.
Sensibilità: P che un malato risulti positivo al test
Specificità: P che un sano risulti negativo al test |
 |
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 16 gennaio 2013 : 19:14:58
|
ESERCIZIO 1:
allora escludendo la penetranza della figlia,mi calcolerei la probabilità che lei abbia ereditato l'allele cosi: 0,31/2*0,55 = 0,0852 (P finale della mamma/2 per la penetranza della mamma.
III,1 portatore Non portatore
P a priori 0,852 - (1-0,852)= 0,148
P condizionale 0,9 - 1
p congiunta 0,077 - 0,148
p finale 0,34 - 0,66
Giusto così??
Problema 2:
A parte che vista la malattia (a penetranza completa mi pare) o è malato o è sano,non è una patologia che insorge tardivamente...comunque proviamoci!
Portatore Non portatore
P a priori 2/3 - 1/3
P condizionale 0,9 - 1
P condizionale specificità 0,15 - 1
e poi continuo con i calcoli....ma non so se è giusto!! |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 17 gennaio 2013 : 01:27:08
|
Citazione:
Messaggio inserito da Daldal
ESERCIZIO 1:
allora escludendo la penetranza della figlia,mi calcolerei la probabilità che lei abbia ereditato l'allele cosi: 0,31/2*0,55 = 0,0852 (P finale della mamma/2 per la penetranza della mamma
Ma scusa perchè hai considerato ancora la penetranza della mamma? l'hai già considerata prima e hai già calcolato la P che la mamma sia portatrice!
Per il secondo, no non mi sembra corretto, però scusa lo riguardo domani. |
|
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 17 gennaio 2013 : 11:02:25
|
Esercizio 1: ho capito GFPina...grazie!! Praticamente per la figlia rifaccio Bayes senza considerare la penetranza della madre!E mi è chiaro!
Tuttavia ammettiamo che il problema si fermi a II,3 e che mi chieda se la figlia II,1 abbia ereditato la malattia...la prof ci fa fare bayes come ho fatto e poi per avere la % finale ci fa fare P finale /2 * penetranza malattia! solo in questo caso si moltiplica la P finale per la penetranza?
Esercizio 2: scusami ma non riesco a capire allora..... |
|
|
|
martolina86
Nuovo Arrivato
Prov.: Pisa
Città: Calci
83 Messaggi |
Inserito il - 17 gennaio 2013 : 15:32:14
|
Una volta che hai trovato che 30% è la prob che sia portatore, allora la prob che dia l'allele malato alla figlia è 0,30/2= 0,15
quindi la prob che III-1 sia portatore è
a priori: 0,15 portatore e 0.85 non portatore
condizionale 0,9 portat e 1 non port
congiunta 0,135 portat e 0.85non portat
finale 14%port
giusto? |
|
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 17 gennaio 2013 : 17:02:07
|
| si martolina.......ma il secondo??ho proprio un problema nel comprenderlo! |
|
|
|
martolina86
Nuovo Arrivato
Prov.: Pisa
Città: Calci
83 Messaggi |
Inserito il - 17 gennaio 2013 : 17:20:18
|
| bella domanda!Non ne ho idea=( |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 17 gennaio 2013 : 17:46:24
|
Allora per il primo esercizio:
Citazione:
Esercizio 1: ho capito GFPina...grazie!! Praticamente per la figlia rifaccio Bayes senza considerare la penetranza della madre!E mi è chiaro!
sì la penetranza della madre l'hai considerata già per la madre, ora rifai Bayes considerando la penetranza della figlia.
Citazione:
Tuttavia ammettiamo che il problema si fermi a II,3 e che mi chieda se la figlia II,1 abbia ereditato la malattia...la prof ci fa fare bayes come ho fatto e poi per avere la % finale ci fa fare P finale /2 * penetranza malattia! solo in questo caso si moltiplica la P finale per la penetranza?
In realtà era quello che intendevo io dicendo:
Citazione:
N.B. se questa ultima probabilità la calcoli senza usare bayes (mettendo però la penentranza) in realtà il risultato è molto simile a quello che ottieni con bayes.
Diciamo che:
- se tu hai una figlia III-1 che è fenotipicamente sana (come in questo caso) sarebbe più corretto usare bayes.
La P a priori è P(madre eterozigote)/2
poi aggiungi il dato della penetranza (di III-1 ovviamente) e calcoli tutto con bayes
- se invece la figlia III-1 non è ancora nata e ti si chiede la P che possa nascere una figlia affetta allora la calcoli così:
P(madre eterozigote)/2 * penetranza
in realtà come ti dicevo prima i due valori in questo caso non vengono molto diversi.
Il problema però in un caso del genere è che la penetranza è diversa in base all'età.
Esercizio 2:
Citazione:
A parte che vista la malattia (a penetranza completa mi pare) o è malato o è sano,non è una patologia che insorge tardivamente
sì in realtà è una malattia autosomica recessiva, quello che ti viene chiesto infatti non è la P che gli individui siano malati ma la P che siano portatori.
Io ti ho messo le definizioni generali di sensibilità e specificità, ma in questo caso sarebbero più corrette così:
Sensibilità: P che un malato portatore risulti positivo al test
Specificità: P che un sano non portatore risulti negativo al test
Come vedi una è riferita al "portatore" mentre l'altra al "non portatore", il tuo errore è che nei calcolo di Bayes le hai assegnate entrambe al "portatore".
Tu sai che il soggetto è risultato "negativo" al test e in base a specificità e sensibilità del test vai a modificare di conseguenza le due probabilità, quella che sia portatore e quella che non sia portatore assegnando la P condizionale alla "classe" corretta. Chiaro ora? |
|
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 17 gennaio 2013 : 18:40:47
|
Per il primo esercizio ci sono!! Grazie per la tua chiarezza!!
Per il secondo tu mi hai scritto "Tu sai che il soggetto è risultato "negativo" al test"
invece no lui è risultato positivo al test!!Quindi so che è portatore!ma il problema vuole sapere qual è la P che non sia portatore, quindi negativo!
Io lo imposterei così:
Portatore Non portatore
P a priori 2/3 - 1/3
P condizionale sensibilità 0,9 - 1
P condizionale specificità 1 - 0,85
|
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 17 gennaio 2013 : 18:46:28
|
Ah sì scusa, non mi ricordavo più l'esercizio e non l'ho riletto ero convinta che dicesse che era positivo e che ti chiedesse la P che fosse portatore.
Comunque il senso del ragionamento non cambia, un attimo che ti sistemo al tabella e controllo lo svolgimento! |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 17 gennaio 2013 : 20:17:05
|
Innanzitutto correggiamo questa cosa:
Citazione:
Messaggio inserito da Daldal
... lui è risultato positivo al test!!Quindi so che è portatore!ma il problema vuole sapere qual è la P che non sia portatore, quindi negativo!
No quello che hai scritto è sbagliato, il fatto che sia risultato positaivo al test non ti dà la certezza che sia portatore! (tra l'altro se fossi certo che è portatore la P che sia non portatore sarebbe zero e l'esercizio non avrebbe neanche senso!)
Tu sai che è positivo al test, quindi può essere un "vero positivo" (e quindi portatore) oppure un "falso positivo" (quindi non portatore) e sono queste le due probabilità che devi calcolare.
(ovviamente l'esercizio te ne chiede una sola, in questo caso la P che sia un falso positivo, ma e uguale perchè comunque sia la somma delle due P sarà sempre 1, quindi calcolata una l'altra sarà 1-P)
Un conto è la positività/negatività al test e un altro è il fatto di essere portarore/non portatore (o sano/affetto in altri casi)
Chiara la differenza ora?
Praticamente puoi farti una tabella di questo tipo:
T+ T-
portatore vero pos. falso neg.
sensibilità 1-sensibilità
non port. falso pos. vero neg.
1-specificità specificità
visto che in questo caso il test è risultato positivo quello che ti interessa è la metà sinistra della tabella.
Ok a questo punto riesci a vedere da solo l'errore che hai fatto nell'impostazione di bayes? |
|
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 17 gennaio 2013 : 21:15:25
|
Portatore Non portatore
P a priori 2/3 - 1/3
P condizionale sensibilità 0,9 - 1
P condizionale specificità 1 - 0,15
Spero che ora sia giusto! |
|
|
|
GFPina
Moderatore
Città: Milano
8408 Messaggi |
Inserito il - 17 gennaio 2013 : 22:03:58
|
Sì ok, ora è giusto!  |
|
|
|
Daldal
Nuovo Arrivato
35 Messaggi |
Inserito il - 17 gennaio 2013 : 22:13:44
|
Grazie GFPina...anche per la pazienza!! Ti devo tanto!!  |
|
|
| |
Discussione |
|
esercizio 
