Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
xgabrix
Nuovo Arrivato

82 Messaggi |
 Inserito il - 04 giugno 2014 : 10:44:37 Inserito il - 04 giugno 2014 : 10:44:37




|
Ciao a tutti,
volevo chiedere un consiglio su quale tipo di analisi statistica é meglio fare se voglio mostrare che la disposizione di 60 individui (tra i quali sono presenti solo 4 aplotipi):
1) non é random
2) che individui con un certo aplotipo hanno una certa tendenza a disporsi nella regione geografica di studio.
Che ne pensate?
Io ho a disposizione Aplotipo e coordinate geografiche di ciascun individuo.
Grazie!!! 
|
|
|
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 04 giugno 2014 : 10:58:07 Inserito il - 04 giugno 2014 : 10:58:07




|
L'ottimo libro: "Randomization, Bootstrap and Monte Carlo Methods in Biology" ha due capitoli (9 e 10) dedicati a questo tipo di problemi.
Confesso che non li ho mai letti nel dettaglio...
Io, in maniera molto naïve procederei così:
1) trova le distanze fra tutti gli individui (1 vs 2, 1 vs 3, ..., 1 vs 60, poi 2 vs 3, 2 vs 4, ... etc).
2) Fai un'istogramma delle distanze, per tutti gli individui e poi per individui di ciascun aplotipo
Se gli individui sono distribuiti indipendentemente tra loro la distribuzione sarà poissoniana, altrimenti potresti avere più mode, corrispondenti ai vari aplotipi.
3) A questo punto puoi fare un test di permutazione, mischiando in modo casuale gli aplotipi e ripetendo il procedimento un grande numero di volte (es 1000) per mostrare che i dati reali sono statisticamente differenti da quelli random.
Ti consiglio vivamente di cercare quel libro tuttavia, perchè penso che spieghi le cose in maniera molto precisa. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 05 giugno 2014 : 10:30:31 Inserito il - 05 giugno 2014 : 10:30:31




|
Ho fatto una piccola simulazione di quanto scritto sopra.
Guarda questo grafico:
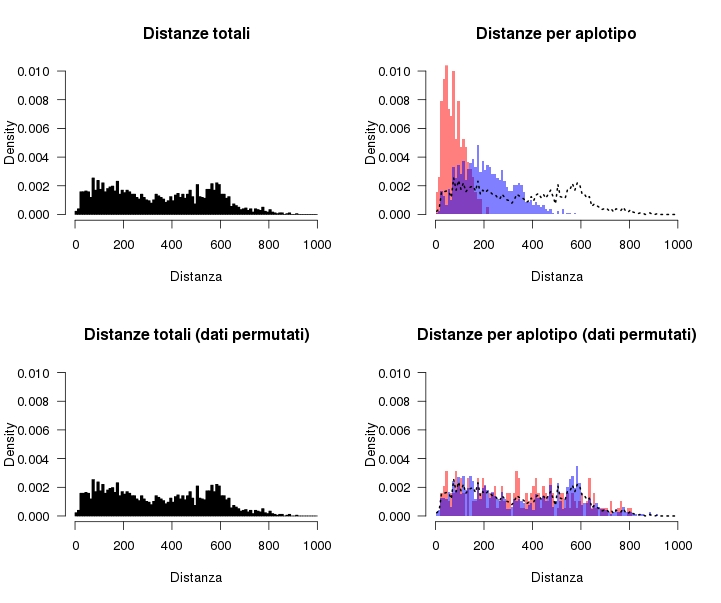
A sinistra hai l'istogramma delle distanze tra tutti i punti, indipendentemente dall'aplotipo, nei dati reali in alto (beh, sono simulati in questo esempio, ma è lo stesso) e nei dati in cui gli aplotipi sono mischiati in basso. Ovviamente visto che le coordinate non cambiano le due distribuzioni sono identiche.
Se però guardi i grafici a destra, che mostrano gli istogrammi per ciascun aplotipo vedi come nei dati permutati la distribuzione delle distanze in ciascun aplotipo è comparabile a quella globale (linea tratteggiata) mentre nei dati reali hai un solo picco distinto a distanze più basse.
Questo significa che i campioni con lo stesso aplotipo sono vicini tra loro, ma se li mischi ottieni un secondo picco a distanze più alte che corrisponde alle distanze fra punti di aplotipo opposto.
Ha senso? |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
xgabrix
Nuovo Arrivato

82 Messaggi |
 Inserito il - 05 giugno 2014 : 12:34:11 Inserito il - 05 giugno 2014 : 12:34:11




|
Mi é piaciuta molto questa simulazione e rispecchia molto bene l'esempio..e ha assolutamente senso quello che scrivi. Aggiungerei che il modo migliore per statisticamente convalidare la disposizione non random degli individui, sarebbe di confrontare una statistica sommaria della distribuzione, per esempio, di uno degli aplotipi, con una distribuzione di statistiche sommarie,ottenuta eseguendo "n" permutazioni.
Cosa ne pensi?
P.S. conosci qualche software semplice che mi permetta di fare tutte queste analisi; e che magari anche a partire da coordinate GPS sia capace di costruirmi una matrice di distanze?
|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 05 giugno 2014 : 22:00:29 Inserito il - 05 giugno 2014 : 22:00:29




|
Sì, ovviamente devi fare molte permutazioni perchè la cosa abbia senso.
L'esempio di sopra l'ho fatto con R.
In quel caso ho ovviamente semplicemente considerato delle coordinate cartesiane, ma esistono vari pacchetti per R contenenti funzioni per trattare dati GPS/spaziali.
Questa pagina è ricca di informazioni a riguardo: http://cran.r-project.org/web/views/Spatial.html |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-24 MolecularLab.it |
 |
|
|





