Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
AlessandroPP
Nuovo Arrivato
4 Messaggi |
 Inserito il - 19 maggio 2013 : 14:08:09
|
Salve a tutti, sono nuovo e vorrei porvi un quesito.
Sono interno in chirurgia, ho raccolto dati relativi alla quantità di liquido prodotta giornalmente, e per 11 giorni, dal drenaggio addominale peripancreatico di 19 pazienti sottoposti ad intervento di duodenocefalopancreasectomia. I pazienti sono suddivisi in due gruppi sulla base di una diversa tecnica chirurgica: 9 in un gruppo e 10 nell'altro. Per ogni paziente ho i valori del liquido drenato in 11 giornate, dalla prima alla undicesima post-operatoria. Ho quindi 19 serie complessive da 11 valori quotidiani di liquido drenato. In entrambi i gruppi è evidente la riduzione della quantità di liquido col passare dei giorni. Applicando 11 test t-student ho dimostrato che per tutte le 11 giornate la media dei liquidi drenati in un gruppo è significativamente diversa da quella dell'altro gruppo. Esiste un test per dimostrare che il trend dei valori in ciascun gruppo differisce? Cioè se un gruppo "drena" meno dell'altro o smette di produrre grandi quantità di liquido più precocemente? Mi piacerebbe analizzare non solo la quantità di liquido ma in pratica anche la velocità della produzione del liquido.
Grazie a tutti!
|
|
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 19 maggio 2013 : 20:54:41
|
Citazione:
Applicando 11 test t-student ho dimostrato che per tutte le 11 giornate la media dei liquidi drenati in un gruppo è significativamente diversa da quella dell'altro gruppo
Questo è scorretto, in quanto ricadi nel problema dei confronti multipli (vedi as es.: https://en.wikipedia.org/wiki/Multiple_comparisons ).
Facendo 11 t-test indipendenti potresti trovare delle differenze che sono solo dovute al caso.
La cosa si complica ulteriormente in quanto le misure sono prese dagli stessi pazienti, quindi devi anche considerare il fattore "paziente" (ad es. un paziente potrebbe avere valori sempre più alti di un altro, ma la velocità di diminuzione della quantità di liquido drenato potrebbe essere la stessa.
Per risolvere il primo problema (confronti multipli) hai 2 opzioni:
1) applichi una correzione come ad es. la correzione di Bonferroni per cui dividi il tuo livello di significatività per il numero di test. Ad es. se hai α=0.05 e fai 11 test dovrai settare il tuo α a 0.05/11 ~= 0.004
2) (meglio) usi un'analisi della varianza (ANOVA) che quindi tiene in considerazione tutti i punti allo stesso tempo.
In particolare (e questo ti serve per risolvere il secondo problema) dovrai applicare un'ANOVA a misure ripetute.
La terza soluzione, che è la migliore, è in realtà quella di applicare un modello lineare ad effetti misti (vedi ad es.: http://en.wikipedia.org/wiki/Mixed_model )
Se vuoi posso farti un esempio di come creare un modello di questo tipo usando R. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
Glubus
Utente Junior
156 Messaggi |
Inserito il - 20 maggio 2013 : 08:11:14
|
Giustissimo chick80!
Due ulteriori osservazioni:
1) il modello di regressione lineare ad effetti misti è la procedura da preferire perché permette di stimare l'effetto del tempo, del trattamento e della loro interazione.
Una certa attenzione dovrà essere però posta alla linearità della risposta nel tempo ed alla omogeneità delle varianze (è possibile che la variabilità sia maggiore alle prime osservazioni e più piccola verso l'undicesima giornata, quando il volume di drenato sarà probabilmente più piccolo).
2) i risultati saranno validi solo se l'allocazione dei pazienti al trattamento è stata casuale. Se invece il trattamente è stato scelto sulla base delle indicazioni cliniche allora le conclusioni dovranno essere prese con un certa cautela.
Per quel che riguarda il punto 1 il consiglio è sempre quello di consultare uno statistico perchè il problema è un po' più complesso che eseguire una batteria di t-test.
Del resto non credo che ti faresti fare una appendicectomia da un biostatistico ;-) !
Citazione:
Messaggio inserito da chick80
Citazione:
Applicando 11 test t-student ho dimostrato che per tutte le 11 giornate la media dei liquidi drenati in un gruppo è significativamente diversa da quella dell'altro gruppo
Questo è scorretto, in quanto ricadi nel problema dei confronti multipli (vedi as es.: https://en.wikipedia.org/wiki/Multiple_comparisons ).
Facendo 11 t-test indipendenti potresti trovare delle differenze che sono solo dovute al caso.
La cosa si complica ulteriormente in quanto le misure sono prese dagli stessi pazienti, quindi devi anche considerare il fattore "paziente" (ad es. un paziente potrebbe avere valori sempre più alti di un altro, ma la velocità di diminuzione della quantità di liquido drenato potrebbe essere la stessa.
Per risolvere il primo problema (confronti multipli) hai 2 opzioni:
1) applichi una correzione come ad es. la correzione di Bonferroni per cui dividi il tuo livello di significatività per il numero di test. Ad es. se hai #945;=0.05 e fai 11 test dovrai settare il tuo #945; a 0.05/11 ~= 0.004
2) (meglio) usi un'analisi della varianza (ANOVA) che quindi tiene in considerazione tutti i punti allo stesso tempo.
In particolare (e questo ti serve per risolvere il secondo problema) dovrai applicare un'ANOVA a misure ripetute.
La terza soluzione, che è la migliore, è in realtà quella di applicare un modello lineare ad effetti misti (vedi ad es.: http://en.wikipedia.org/wiki/Mixed_model )
Se vuoi posso farti un esempio di come creare un modello di questo tipo usando R.
 |
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 20 maggio 2013 : 09:02:52
|
Faccio solo una piccola correzione a quanto ho scritto sopra:
Citazione:
Facendo 11 t-test indipendenti potresti trovare delle differenze che sono solo dovute al caso.
In realtà questo è vero anche se ne fai uno solo. Tuttavia, facendone 11 hai molta più probabilità di vedere delle differenze che sono in realtà solo dovute al caso.
Ne approfitto anche per linkare questo simpatico esempio del problema: http://xkcd.com/882/ |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
AlessandroPP
Nuovo Arrivato
4 Messaggi |
Inserito il - 20 maggio 2013 : 18:57:16
|
Grazie per i preziosi consigli!
Prima di tutto preciso che la scelta dell'intervento chirurgico non è casuale, dato che le due tecniche si sono succedute cronologicamente: 10 pazienti sono stati operati con la tecnica più antica, 9 con una nuova tecnica introdotta da qualche anno.
Ho applicato sia una ANOVA a misure ripetute che una regressione lineare ad effetti multipli con STATA 12. Purtroppo non conosco R anche se sto cercando di ambientarmici. In allegato trovate i risultati che ho ottenuto, da cui, ammesso che non abbia sbagliato impostazioni (dubbio che ho soprattutto per la regressione lineare ad effetti multipli per la quale consulterò uno statistico  ) e tenuto presente che il trattamento non è casuale, mi sembra di concludere che le variabili Giorno e Trattamento (Impact1trad0) abbiano un peso maggiore della variabile Paziente nel determinare il volume drenato.
Grazie ancora!
Allegato:  drenaggi pancreatici risultati.doc
93,94 KB |
|
|
|
Glubus
Utente Junior
156 Messaggi |
Inserito il - 21 maggio 2013 : 08:39:35
|
Mah? Non sono pratico di STATA ma comprendro il significato del termine "paziente" nella tavola degli effetti fissi della seconda analisi e sospetto possa esserci un problema concettuale.
Le due analisi sono comunque concettualmente diverse: nel modello di regressione ad effetti MISTI ad esempio la variabile giorno è modellata continua e non come discreta e questo sottointende una assunzione di linearità fra giorno e volume drenato.
Come lo hai verificato? Un grafico direbbe molto su questi dati.
In ogni caso credo dovresti testare anche l'interazione giorno*tipo di intervento.
I modelli ad effetti misti sono un ambito abbastanza avanzato, quele è il tuo background in statistica? Ad esempio, sempre all'intero del ME model dovresti pensare a come modellare la autocorrelazione seriale (la correlazione fra le misure ripetute nel tempo sugli stessi sogegetti) ed avere a disposizione un software ed un manuale potrebbe non essere sufficiente, ...
Ti propongo un semplice escamotage per risparmiare sullo statistico: fai semplicemente la somma del volume denato giornaliero per ogni paziente fino alla rimozione del drenaggio ed esegui un semplice t-test ( o l'analogo test non-parametrico se necessario) su queste osservazioni. In questo modo eviti tutte queste complicazioni legate alle misure ripetute.
GB
Citazione:
Messaggio inserito da AlessandroPP
Grazie per i preziosi consigli!
Prima di tutto preciso che la scelta dell'intervento chirurgico non è casuale, dato che le due tecniche si sono succedute cronologicamente: 10 pazienti sono stati operati con la tecnica più antica, 9 con una nuova tecnica introdotta da qualche anno.
Ho applicato sia una ANOVA a misure ripetute che una regressione lineare ad effetti multipli con STATA 12. Purtroppo non conosco R anche se sto cercando di ambientarmici. In allegato trovate i risultati che ho ottenuto, da cui, ammesso che non abbia sbagliato impostazioni (dubbio che ho soprattutto per la regressione lineare ad effetti multipli per la quale consulterò uno statistico ) e tenuto presente che il trattamento non è casuale, mi sembra di concludere che le variabili Giorno e Trattamento (Impact1trad0) abbiano un peso maggiore della variabile Paziente nel determinare il volume drenato.
Grazie ancora!
Allegato: drenaggi pancreatici risultati.doc
93,94 KB
|
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 21 maggio 2013 : 09:56:50
|
Concordo con Glubus.
In realtà la cosa migliore sarebbe ovviamente avere accesso ai dati grezzi per darti una risposta più chiara.
Un ultimo commento:
Citazione:
Prima di tutto preciso che la scelta dell'intervento chirurgico non è casuale, dato che le due tecniche si sono succedute cronologicamente: 10 pazienti sono stati operati con la tecnica più antica, 9 con una nuova tecnica introdotta da qualche anno.
In realtà questo è un problema relativamente facile da risolvere. Il grosso problema sarebbe stato, ad es., se i 10 pazienti operati col metodo 1 fossero stati tutti uomini e gli altri 9 tutte donne, oppure se quelli di un gruppo fossero stati sistematicamente più giovani di quelli dell'altro gruppo etc.
In questo caso anche se in effetti i due trattamenti non sono stati eseguiti allo stesso tempo, correggimi se sbaglio, le caratteristiche dei pazienti (età, sesso, gravità della malattia etc.) sono equiparabili nei due gruppi quindi anche se il design non è ottimale direi che -a patto di riportare che i due trattamenti non sono stati fatti nello stesso periodo- questo non dovrebbe porre un grosso problema.
Faccio una piccola parentesi teorica per chiarire un po' meglio di cosa stiamo parlando:
Quando generi un modello lineare dai tuoi dati quello che fai matematicamente è questo:
Cosa vuol dire:
y è la tua variabile osservata, nel tuo caso la quantità di drenato
β sono i fattori fissi, ossia tutte le variabili che contribuiscono direttamente e non "casualmente" alla generazione di y. Nel tuo caso saranno il tipo di trattamento e il giorno del prelevamento (essendo y più grande il giorno 1 rispetto al giorno 2 o 3 etc.). In realtà io qui ci aggiungerei anche dei fattori come il sesso e l'età (e magari qualche livello ormonale?) che penso potrebbero essere biologicamente interessanti da considerare, ma su questo lascio a te la parola.
u sono gli effetti casuali (random o nuisance factors). Queste sono le variabili che contribuiscono più "casualmente" alla generazione di y. Nota che casualmente non vuol dire che la cosa non sia deterministica, ma più che altro che tu non hai direttamente controllo su queste variabili e che quindi non fanno direttamente parte del tuo disegno sperimentale.
Nel nostro esempio il paziente sarà considerato come random factor.
X e Z sono dei fattori che definiscono l'importanza dei vari effetti. In pratica se il tuo modello fosse:
quantità di drenato = X * giorno + Z * paziente + ε
Se il fattore giorno è molto più importante del fattore paziente allora X sarà (in valore assoluto) molto più importante di Z.
Infine ε è il termine di errore, che se vuoi rappresenta tutto quello che non hai misurato. Ad es. la temperatura dell'aria, la pressione, etc. etc. etc.
Insomma, l'idea è che se io calcolo:
drenato = X * giorno + Z * paziente
Otterrò dei valori di drenato che sono in generale diversi da quelli misurati realmente (ricorda, stiamo generando un modello).
ε sarà quindi uguale a:
ε = drenato(reale) - drenato(calcolato)
ossia la differenza fra il modello e la realtà.
Quando tu chiedi al tuo programma di statistica di generare il modello, quello che lui fa è di trovare dei valori di X e Z tali da minimizzare questo errore. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
AlessandroPP
Nuovo Arrivato
4 Messaggi |
Inserito il - 21 maggio 2013 : 12:32:01
|
Che posso dire... Grazie davvero per la completezza delle risposte! Grazie per aver sottolineato gli errori della mia analisi e per avermi rassicurato sulla non casualità dell'assegnazione del trattamento (in effetti sesso ed età sono confrontabili, altre variabili come l'albuminemia pre e post intervento sono in corso di raccolta). Allego i dati grezzi. Comunque senza abusare della vostra pazienza credo che per il momento mi limiterò al t-student sui totali drenati o al massimo all'ANOVA per misure ripetute. Grazie per il presupposto teorico del modello di regressione lineare ad effetti misti, mi è abbastanza chiaro, ma devo studiare come tradurre per bene il tutto in STATA.
La mia formazione statistica è assolutamente di base (esame di statistica al terzo anno del mio corso di laurea in Medicina e Chirurgia), ma sono un "appassionato" che fino ad ora si era cimentato solo con confronti di medie e proporzioni in ricerche che spero vedano la luce al più presto, appena ho un attimo scrivo il curriculum.
Allegato: drenaggi pancreatici dati.xlsx
13,35 KB |
|
|
|
Glubus
Utente Junior
156 Messaggi |
Inserito il - 21 maggio 2013 : 12:58:06
|
guarda intanto questo grafico ("spaghetti plot"). Il pannello a sinistra rappresenta il trattamento convenzionale e le traiettorie colorate sono i dati individuali. Come vedi già la linearità sarebbe questionabile, poi nota come la varianza diminuisca con il livello.
GB
Citazione:
Messaggio inserito da AlessandroPP
Che posso dire... Grazie davvero per la completezza delle risposte! Grazie per aver sottolineato gli errori della mia analisi e per avermi rassicurato sulla non casualità dell'assegnazione del trattamento (in effetti sesso ed età sono confrontabili, altre variabili come l'albuminemia pre e post intervento sono in corso di raccolta). Allego i dati grezzi. Comunque senza abusare della vostra pazienza credo che per il momento mi limiterò al t-student sui totali drenati o al massimo all'ANOVA per misure ripetute. Grazie per il presupposto teorico del modello di regressione lineare ad effetti misti, mi è abbastanza chiaro, ma devo studiare come tradurre per bene il tutto in STATA.
La mia formazione statistica è assolutamente di base (esame di statistica al terzo anno del mio corso di laurea in Medicina e Chirurgia), ma sono un "appassionato" che fino ad ora si era cimentato solo con confronti di medie e proporzioni in ricerche che spero vedano la luce al più presto, appena ho un attimo scrivo il curriculum.
Allegato: drenaggi pancreatici dati.xlsx
13,35 KB
Immagine:
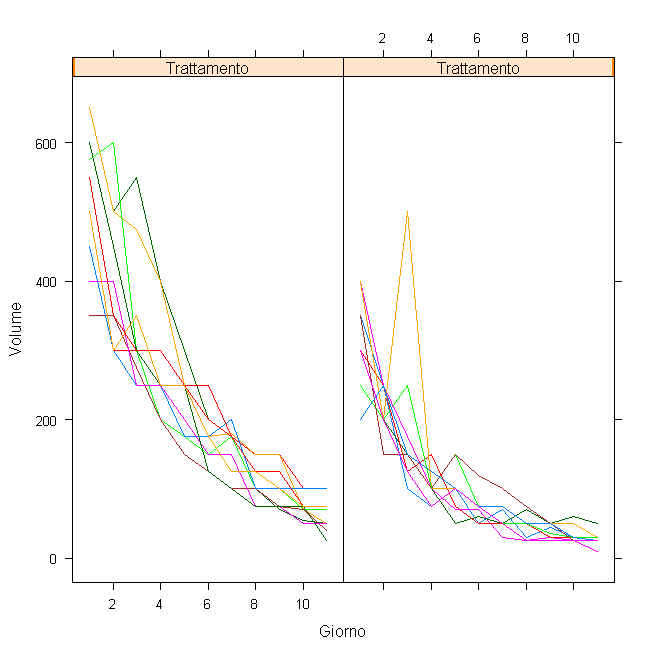
10,42 KB |
|
|
|
TMax
Utente Junior
Prov.: BG
Città: Capriate
270 Messaggi |
Inserito il - 22 maggio 2013 : 11:11:46
|
u sono gli effetti casuali (random o nuisance factors). Queste sono le variabili che contribuiscono più "casualmente" alla generazione di y. Nota che casualmente non vuol dire che la cosa non sia deterministica, ma più che altro che tu non hai direttamente controllo su queste variabili e che quindi non fanno direttamente parte del tuo disegno sperimentale.
Nel nostro esempio il paziente sarà considerato come random factor.
Ciao Chick,
una precisazione....circa i fattori ad effetti random; non credo sia corretto affermare che sono quelli che contribuiscono più casualmente al variabilità di y.
Il termine random si riferisce ai livelli del fattore.
Mentre nei fattori ad effetti fissi i livelli sono in genere pochi e invarianti e sono quelli che interessano al ricercatore (o per lo meno la differenza tra i diversi livelli del fattore è una differenza che interessa!).
Ad esempio: fattore trattamento con due livelli di interesse A e B
in questo caso non ci sono dubbi: esistono solo quei due livelli e la loro differenza è il focus dello studio.
Nei fattori ad effetti random i livelli sono un 'campione rappresentativo' dell'universo dei possibili livelli che può assumere la variabile. Non è d'interesse studiare le differenze tra questi livelli.
Ad esempio: fattore paziente è un fattore con un numero di livelli che è determinato dal disegno dello studio, quei livelli cioè pazienti sono solo un campione casuale dell'universo possibile dei pazienti.
In questo caso la componente di variabilità di Y dovuta a questo fattore è una componente da controllare per ottenere una migliore spiegazione della variabilità di Y....
Ciao |
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 22 maggio 2013 : 14:02:26
|
Grazie della precisazione TMax. Ho messo quel casualmente tra virgolette proprio per quello.
La tua spiegazione è più chiara in effetti!
Era un po' quello che volevo dire dicendo che questi fattori "non fanno parte del tuo disegno sperimentale". |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-18 MolecularLab.it |
|
|
|
Confronto trend di variabili continue
Guide tools online
