Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
sea
Nuovo Arrivato
Prov.: Lecce
Città: lecce
19 Messaggi |
 Inserito il - 22 febbraio 2014 : 21:33:06
|
Ciao a tutti!
Ho analizzato la concentrazione degli ioni calcio con due diversi metodi(Volumetrico e Gravimetrico). Ho applicato poi i test statistici F-test e t-test, trovando che le deviazioni standard sono differenti, mentre le medie sono uguali. Come posso interpretare questi riusltati?
Grazie mille per il vostro aiuo.
|
|
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
|
|
sea
Nuovo Arrivato
Prov.: Lecce
Città: lecce
19 Messaggi |
Inserito il - 24 febbraio 2014 : 00:29:44
|
Si`, ho analizzato lo stesso ampione di Calcio con due diversi metodi (gravimetico e volumetrico).
Che tipo di grafico intendi? "Ad ogni modo, la cosa migliore da fare (regola generale) è quella di cominciare a fare un grafico dei dati e vedere cosa i dati ti dicono."
Comunque non penso che il mio Prof. voglia andare cosi` nello specifico, con la l'inserimento di un tale grafico nel long Lab report che dovro` presentargli. (sono in un' Universita` Americana a seguire un Corso di Chimica Analitica.
Potresti spiegarmi meglio questa tua conclusione: "Il t-test ti dirà essenzialmente che le tue misure sono equivalenti in termini di precisione. Tuttavia, se le varianze sono diverse vuol dire probabilmente che uno dei due metodi è meno accurato dell'altro, o che c'è un bias di qualche tipo." |
 |
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 24 febbraio 2014 : 09:12:30
|
Allego un paio di grafici di esempio
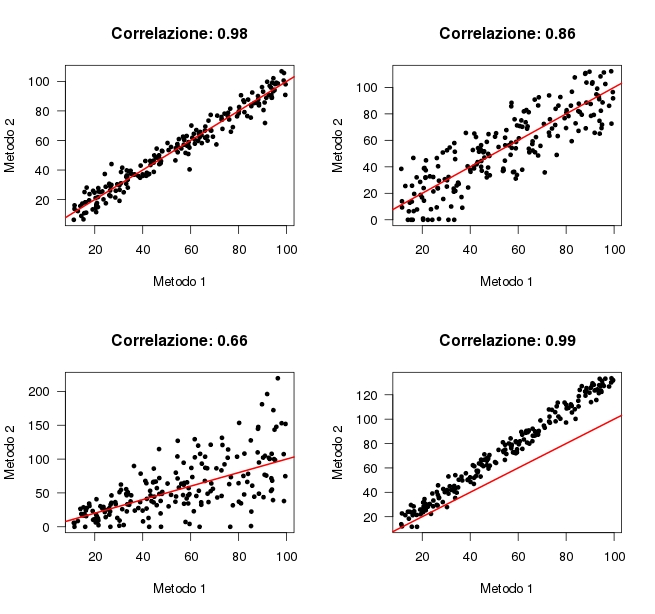
Nell'immagine hai quattro grafici di quattro ipotetiche situazioni, in cui ogni punto rappresenta un campione, con coordinate rappresentanti i valori ottenuti dalle due misurazioni. In rosso ho messo la retta y=x e ho calcolato la correlazione di Pearson per ciascun caso.
Se le due misure sono in accordo i valori seguiranno la retta y=x, in quanto i due metodi daranno, in media, lo stesso valore per lo stesso campione.
Nel primo caso i due metodi sembrerebbero essere equivalenti, in quanto le misure non si discostano molto dalla retta. La correlazione è molto alta (ricorda, la correlazione va da 0 a 1, qui siamo a 0.98!).
Nel secondo caso la correlazione è ancora alta, i metodi seguono la retta, ma i valori sono molto più dispersi. Questo vuol dire che uno dei due metodi è meno preciso dell'altro.
Il terzo caso è come il secondo, ma in questo caso l'aumento di varianza lo vedi soprattutto per valori alti. Questo è chiaro sia graficamente, che dal valore di correlazione che scende a 0.66
L'ultimo caso ti mostra due metodi con la stessa precisione, e che danno misure estremamente correlate. In questo caso però uno dei due metodi sovrastima la misura rispetto all'altro (o, viceversa, uno dei due metodi sottostima la misura).
Questo ultimo caso ti mostra come sia importante non fidarsi ciecamente della correlazione (o del risultato del t-test etc). La correlazione è altissima, ma i metodi non sono equivalenti.
Andiamo ora a fare un grafico dei valori in formato di boxplot.
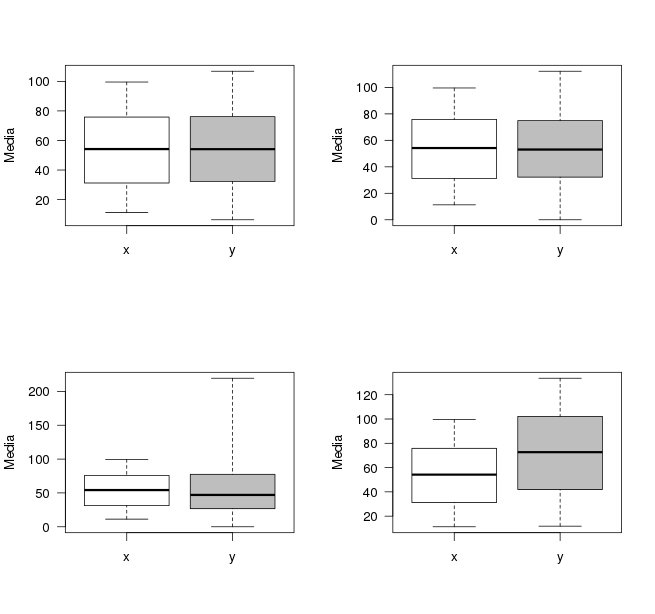
In questo caso vediamo bene che nel quarto caso c'è una sovrastima del metodo y rispetto a x e notiamo bene l'aumento di varianza nel caso 3, ma non nel caso 2.
Un paired t-test ci dice che nei casi 1 2 e 3 x e y non sono statisticamente differenti, mentre lo sono nel caso 4 (p-values, sono 0.992, 0.581, 0.267 e 0.000). Questo riflette il fatto che nei primi tre casi le misure si aggirano attorno alla famosa retta y=x.
Nota che questo è equivalente a fare un t-test univariato sulle differenze, ossia testare se le differenze sono diverse da 0 (matematicamente se x/y=1 allora x-y=0).
L'analisi della varianza ci dà ancora una volta lo stesso risultato del test t, con p-values 0.992, 0.581, 0.267 e 0.000. Questo tuttavia non è un test appaiato e semplicemente ti dice che, sotto l'ipotesi (falsa nel caso specifico) che i campioni siano presi da una distribuzione normale, le varianze dei campioni non sono statisticamente differenti nei primi 3 casi.
Citazione:
Comunque non penso che il mio Prof. voglia andare cosi` nello specifico
Questo lo sai meglio tu di me :)
Ad ogni modo meglio essere cosciente di queste cose (e saper rispondere ad eventuali domande a riguardo) che ignorarle completamente. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
sea
Nuovo Arrivato
Prov.: Lecce
Città: lecce
19 Messaggi |
Inserito il - 24 febbraio 2014 : 15:11:58
|
Thank you very very very much.
Adesso, potresti spiegarmi meglio questa tua conclusione: "Il t-test ti dirà essenzialmente che le tue misure sono equivalenti in termini di precisione. Tuttavia, se le varianze sono diverse vuol dire probabilmente che uno dei due metodi è meno accurato dell'altro, o che c'è un bias di qualche tipo." |
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 24 febbraio 2014 : 19:41:18
|
Scusami, ho scambiato i due termini sopra...
Rileggi la frase come:
Citazione:
Il t-test ti dirà essenzialmente che le tue misure sono equivalenti in termini di accuratezza. Tuttavia, se le varianze sono diverse vuol dire probabilmente che uno dei due metodi è meno preciso dell'altro, o che c'è un bias di qualche tipo.
In sostanza è più o meno quello che ti ho scritto sopra.
L'accuratezza misura la deviazione di un metodo dal valore vero. Ad es. se nella tua soluzione hai 0.100mM di calcio (valore vero) e i due metodi ti riportano lo stesso valore (es. metodo 1: 0.112, metodo 2: 0.113) i metodi sono ugualmente accurati. Nota che sarebbero ugualmente accurati anche se ti dessero entrambi 50, solo che avrebbero entrambi un'accuratezza molto bassa.
Nota che questo è equivalente a dire che i valori nel grafico di cui sopra sono sulla famosa retta y=x (o che le differenze stanno su y=0 nel grafico di Bland-Altman).
La precisione indica la ripetibilità del metodo, ossia la dispersione di misure ripetute. Ad es. se misuro 3 volte il mio campione a 0.1M un metodo preciso ed accurato mi darà 0.11, 0.09, 0.12 oppure un metodo preciso ma non accurato darà 1.5, 1.48, 1.52.
La varianza delle misure ti dà un'idea di questa cosa (vedi grafici di sopra, sempre con tutti i caveat del caso, ribadisco che personalmente non farei un F-test in questo caso).
Magari uno dei nostri cari statistici può chiarire meglio questi punti? |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
sea
Nuovo Arrivato
Prov.: Lecce
Città: lecce
19 Messaggi |
Inserito il - 24 febbraio 2014 : 21:08:45
|
| Sì grazie..vorrei capire come posso interpretare meglio, a cosa possono essere dovuti e come migliorare questi miei risultati:dopo l'applicazione dei test statistici F-test e t-test, le devHiazioni standard sono differenti, mentre le medie sono uguali. |
|
|
|
Glubus
Utente Junior
156 Messaggi |
Inserito il - 25 febbraio 2014 : 09:15:31
|
Come ti è stato suggerito, cerca "Bland Altman" con google. Faccio anche notare l'assoluta inutilità della misura della correlazione lineare: sappiamo già che le misure sono correlate (e a maggior ragione un test sull'ipotesi H0: rho=0 non ha davvero senso) e spesso la relazione fra le risposte ai due test non è lineare. Inoltre può essere utile sapere se la varianza delle differenze fra i due test sia stabile o dipenda (come spesso accade) dal livello dell'analita.
Il metodo di BA, che è essenzialmente grafico, evidenzia queste caratteristiche. Non ha invece nessun senso un t-test perchè i dati NON sono indipendenti.
Citazione:
Messaggio inserito da sea
Ciao a tutti!
Ho analizzato la concentrazione degli ioni calcio con due diversi metodi(Volumetrico e Gravimetrico). Ho applicato poi i test statistici F-test e t-test, trovando che le deviazioni standard sono differenti, mentre le medie sono uguali. Come posso interpretare questi riusltati?
Grazie mille per il vostro aiuo.
|
|
|
|
chick80
Moderatore
Città: Edinburgh
11491 Messaggi |
Inserito il - 25 febbraio 2014 : 16:39:40
|
| Glubus, tuttavia io farei un t-test univariato sulle differenze... che è poi quello che guardi nel grafico di Bland-Altman (ossia, che la differenza fra i due metodi sia ~0, che equivale a dire che il rapporto sia ~1). |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
|
|
|
Glubus
Utente Junior
156 Messaggi |
Inserito il - 25 febbraio 2014 : 20:10:46
|
Si, il test sulle differenze equivale al t-test per dati appaiati e qui è applicabile ma rispetto al B-A tace sugli aspetti più rilevanti (linearità, omogeneità della varianza dlle differenze, ...), a parte il problema di potenza (quanto è una differenza "importante").
Le due ipotesi nulle sulla differenza (H0=0) e sul rapporto (H0=1) non sono equivalenti: il test sull'ipotesi nulla H0:rapporto=1 equivale al test H0=0 sulle differenze dei logaritmi, cosa utile se le differenze dipendono (aumentano) col livello dell'analita e nel grafico di BA lo scatterplot forma un "imbuto". Anche qui però l'interpretazione non può prescindere da una conoscenza del dominio.
GB
Citazione:
Messaggio inserito da chick80
Glubus, tuttavia io farei un t-test univariato sulle differenze... che è poi quello che guardi nel grafico di Bland-Altman (ossia, che la differenza fra i due metodi sia ~0, che equivale a dire che il rapporto sia ~1).
|
|
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-18 MolecularLab.it |
|
|
|
F-test e t-test
Guide tools online
