Quanto è utile/interessante questa discussione:
| Autore |
Discussione |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 21 marzo 2014 : 08:40:13 Inserito il - 21 marzo 2014 : 08:40:13




|
Ciao a tutti,
ho una serie di dati bivariati in cui devo stimarne la distribuzione congiunta. Tali dati sono due segnali in cui il primo, che chiamo A può assumere esclusivamente i valori 0,1,2,3,4,5, mentre l'altro, che chiamo B, può assumere con continuità i valori compresi tra 0 e 3000 , tuttavia è pratica ingegneristica discretizzarlo attraverso la suddivisione in intervalli che posso scegliere a mio piacimento. Lo scopo di questo lavoro è quello di estrapolare i valori estremi assunti da B che potrei non aver misurato a causa della loro bassa probabilità di occorrenza, tuttavia B è dipendente da A e pertanto pensavo di stimarne la distribuzione congiunta. Trovo difficoltà a stimarla in questo caso perchè A non può assumere un valore diverso al di fuori dall'intervallo di misura e quindi utilizzando i "classici" metodi (fitting con una distribuzione parametrica o non parametrica) potrei ottenere anche un valore di A pari 6 che in realtà è irrealistico. Avete un qualche suggerimento da darmi per calcolare la distribuzione congiunta delle tra le due variabili?
Grazie :)
|
|
|
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 22 marzo 2014 : 18:42:11 Inserito il - 22 marzo 2014 : 18:42:11




|
| Allora ho trovato qualcosa ma ancora non è abbastanza. In pratica dovrei trovare una distribuzione congiuta che sia discreta e troncata per una variabile e che sia invece continua per l'altra. E' secondo voi possibile fare questa cosa? |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 23 marzo 2014 : 10:02:21 Inserito il - 23 marzo 2014 : 10:02:21




|
Citazione:
Trovo difficoltà a stimarla in questo caso perchè A non può assumere un valore diverso al di fuori dall'intervallo di misura e quindi utilizzando i "classici" metodi (fitting con una distribuzione parametrica o non parametrica) potrei ottenere anche un valore di A pari 6 che in realtà è irrealistico. Avete un qualche suggerimento da darmi per calcolare la distribuzione congiunta delle tra le due variabili?
Scusami, ma se B dipende da A sei tu a definire A...
Io semplicemente utilizzerei un modello lineare (per iniziare, se non basta ci sono modelli più complessi) con cinque variabili dummy per i vari livelli di A (che sarà quindi considerato un fattore con 6 livelli) e una variabile continua per B.
Un esempio in R
# Generiamo valori random di A
A <- sample(0:5, 50, replace=T)
# E i corrispondenti valori di B, lineari in A + un termine d'errore
B <- 300 * A + 3 * rnorm(50, 30, 150)
# Convertiamo A in un fattore con 6 livelli (0, 1, ..., 5)
A <- factor(A)
# Generiamo il nostro modello lineare
model <- lm(B~A)
summary(model)
Call:
lm(formula = B ~ A)
Residuals:
Min 1Q Median 3Q Max
-1191.77 -398.07 -45.15 478.37 986.22
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 139.0 187.5 0.741 0.46247
A1 270.3 258.5 1.046 0.30147
A2 187.8 313.8 0.598 0.55261
A3 741.8 265.2 2.797 0.00761 **
A4 1309.8 252.8 5.180 5.30e-06 ***
A5 1402.2 296.5 4.729 2.35e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 562.6 on 44 degrees of freedom
Multiple R-squared: 0.5112, Adjusted R-squared: 0.4557
F-statistic: 9.204 on 5 and 44 DF, p-value: 4.742e-06
Come vedi vengono create 5 variabili dummy A1, A2, A3, A4, A5 e A=0 è utilizzato come livello di referenza.
|
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 23 marzo 2014 : 10:40:27 Inserito il - 23 marzo 2014 : 10:40:27




|
Citazione:
Messaggio inserito da chick80
Citazione:
Trovo difficoltà a stimarla in questo caso perchè A non può assumere un valore diverso al di fuori dall'intervallo di misura e quindi utilizzando i "classici" metodi (fitting con una distribuzione parametrica o non parametrica) potrei ottenere anche un valore di A pari 6 che in realtà è irrealistico. Avete un qualche suggerimento da darmi per calcolare la distribuzione congiunta delle tra le due variabili?
Scusami, ma se B dipende da A sei tu a definire A...
grazie Chick per la risposta.
Allora credo di essermi espresso male. Io comando A, B in realtà dipende da A e da altri parametri ed il valore massimo raggiungibile da B è dipendente da A.
Citazione:
Io semplicemente utilizzerei un modello lineare (per iniziare, se non basta ci sono modelli più complessi) con cinque variabili dummy per i vari livelli di A (che sarà quindi considerato un fattore con 6 livelli) e una variabile continua per B.
Un esempio in R
# Generiamo valori random di A
A <- sample(0:5, 50, replace=T)
# E i corrispondenti valori di B, lineari in A + un termine d'errore
B <- 300 * A + 3 * rnorm(50, 30, 150)
# Convertiamo A in un fattore con 6 livelli (0, 1, ..., 5)
A <- factor(A)
# Generiamo il nostro modello lineare
model <- lm(B~A)
summary(model)
Call:
lm(formula = B ~ A)
Residuals:
Min 1Q Median 3Q Max
-1191.77 -398.07 -45.15 478.37 986.22
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 139.0 187.5 0.741 0.46247
A1 270.3 258.5 1.046 0.30147
A2 187.8 313.8 0.598 0.55261
A3 741.8 265.2 2.797 0.00761 **
A4 1309.8 252.8 5.180 5.30e-06 ***
A5 1402.2 296.5 4.729 2.35e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 562.6 on 44 degrees of freedom
Multiple R-squared: 0.5112, Adjusted R-squared: 0.4557
F-statistic: 9.204 on 5 and 44 DF, p-value: 4.742e-06
Come vedi vengono create 5 variabili dummy A1, A2, A3, A4, A5 e A=0 è utilizzato come livello di referenza.
Ok grazie. Prima di applicare questo devo convertire le frequenze assolute in relative, giusto? |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 23 marzo 2014 : 12:42:36 Inserito il - 23 marzo 2014 : 12:42:36




|
Citazione:
Allora credo di essermi espresso male. Io comando A, B in realtà dipende da A e da altri parametri ed il valore massimo raggiungibile da B è dipendente da A.
Sì, io mi riferivo al fatto che visto che sei tu a imporre A, questo non sarà mai 6. Tuttavia, hai ragione a dire che un modello inappropriato potrebbe darti B fuori scala.
Citazione:
Ok grazie. Prima di applicare questo devo convertire le frequenze assolute in relative, giusto?
No, io non le normalizzerei.
Ovviamente io qui sto facendo delle assunzioni dovute al fatto che non ho i veri dati in mano.
Nel mio esempio io ho generato B in maniera che fosse linearmente dipendente da A, ma non è detto che ciò sia vero in realtà...
A può essere 0, 1, 2, ..., 5. Questi valori sono arbitrari o hanno un significato numerico? Ad esempio, hai 5 settaggi di intensità su una lampada dove 0=spenta e 5=max della luce oppure sono semplicemente settaggi diversi che avresti potuto chiamare A,B,C,D,E,F? Insomma, l'ordine è importante?
Se potessi dare un'esempio dei dati reali possiamo ragionarci meglio insieme. |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 25 marzo 2014 : 09:53:24 Inserito il - 25 marzo 2014 : 09:53:24




|
Ciao Chick,
grazie per la tua risposta. Allora questo è uno dei tanti set di dati di cui poi devo calcolare la distribuzione di probabilità. bin A sono i valori conteggiati del segnale A mentre Bin_B sono i valori di discretizzazione del segnale B discretizzati.
bin_A
0 1 2 3 4 5 6 7 8 9 10
bin_B
0 - 322 0 0 0 0 632 0 8 0 6 0 0
322 - 644 0 0 0 0 138 0 4 0 4 0 0
644 - 966 0 0 0 0 364 0 20 0 154 0 46
966 - 1288 0 0 0 0 400 0 590 0 857 0 3157
1288 - 1611 0 0 0 0 74 0 63 0 1455 0 21670
1611 - 1933 0 0 0 0 14 0 29 0 1191 0 49360
1933 - 2255 0 0 0 0 0 0 12 0 467 0 12031
2255 - 2577 0 0 0 0 0 0 0 0 0 0 0
2577 - 2900 0 0 0 0 0 0 0 0 0 0 0
>2900 0 0 0 0 0 0 0 0 0 0 0
La discretizzazione viene solitamente fatta per ragioni pratiche ma potrebbe essere evitata. Infatti una cosa che io critico del metodo usuale è proprio la discretizzazione che poteva starci 50 anni fa quando i PC non erano sufficientemente potenti per fare certe analisi ma adesso si potrebbero fare le stesse analisi con il dato continuo. Tuttavia se consideressi entrambe le variabili come discrete la cosa si semplificherebbe non poco.
Come ti sembrano i dati?
grazie mille
|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 26 marzo 2014 : 08:41:59 Inserito il - 26 marzo 2014 : 08:41:59




|
Ma gli 0 sono proprio 0 oppure valori non misurati?
Perchè ad esempio sembrerebbe che le misure per a=5, 7 e 9 siano mancanti... (nota che ho rappresentato la radice quadrata di b)
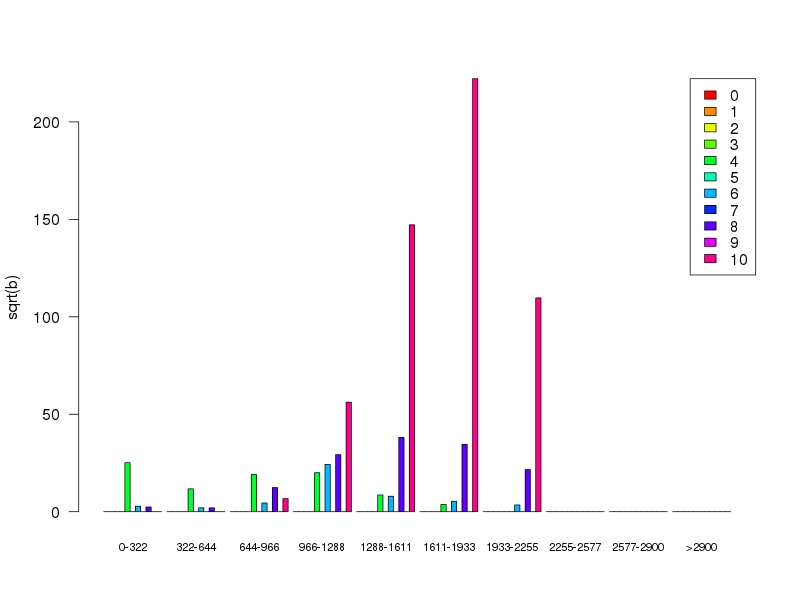
In questo caso mi sembra di capire che a sia una variabile ordinale. Leggiucchiando un po' su Google mi sembra che non ci sia una soluzione definitiva su come utilizzarle in un modello.
Essenzialmente hai due opzioni:
1) la consideri come un fattore (es. usando as.factor in R), il che creerà una serie di variabili dummy e perdi l'informazione sull'ordine delle categorie
2) la consideri come fosse un valore continuo ma questo pone ovviamente vari problemi.
Dalla vignette del package clm che spiega questa cosa nell'introduzione:
Citazione:
Ordinal response variables can be analyzed with omnibus Pearson χ2 tests, base-line logit models or log-linear models. This corresponds to assuming that the response variable is nominal and information about the ordering of the categories will be ignored. Alternatively numbers can be attached to the response categories, e.g., 1,2, . . . , J and the resulting scores can be analyzed by conventional linear regression and ANOVA models. This approach is in a sense over-confident since the data are assumed to contain more information than they actually do. Observations on an ordinal scale are classified in ordered categories, but the distance between the categories is generally unknown. By using linear models the choice of scoring impose assumptions about the distance between the response categories. Further, standard errors and tests from linear models rest on the assumption that the response, conditional on the explanatory variables, is normally distributed (equivalently the residuals
are assumed to be normally distributed). This cannot be the case since the scores are discrete and responses beyond the end categories are not possible. If there are many responses in the end categories, there will most likely be variance heterogeneity to which F and t tests can be rather sensitive. If there are many response categories and the response does not pile up in the end categories, we may expect tests from linear models to be accurate enough, but any bias and optimism is hard to quantify
Ti lascio con queste riflessioni... :D e ci ripenso magari stasera.
Nel frattempo se uno dei nostri cari statistici facesse un giro da queste parti... |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 27 marzo 2014 : 09:30:00 Inserito il - 27 marzo 2014 : 09:30:00




|
Citazione:
Messaggio inserito da chick80
Ma gli 0 sono proprio 0 oppure valori non misurati?
Perchè ad esempio sembrerebbe che le misure per a=5, 7 e 9 siano mancanti... (nota che ho rappresentato la radice quadrata di b)

Ciao Chick,
grazie per la tua risposta.
Allora ho indicato nell'istogramma il numero di volte un certo dato si presenta, quindi per me lo 0 è un dato che è mancante. Dovrei quindi eliminare quei valori? Ho deciso di mettere 0 perchè non sapevo come fare per confrontare poi dati fatti da misure differenti.
Citazione:
In questo caso mi sembra di capire che a sia una variabile ordinale.
Leggiucchiando un po' su Google mi sembra che non ci sia una soluzione definitiva su come utilizzarle in un modello.
Essenzialmente hai due opzioni:
1) la consideri come un fattore (es. usando as.factor in R), il che creerà una serie di variabili dummy e perdi l'informazione sull'ordine delle categorie
2) la consideri come fosse un valore continuo ma questo pone ovviamente vari problemi.
Dalla vignette del package clm che spiega questa cosa nell'introduzione:
Citazione:
Ordinal response variables can be analyzed with omnibus Pearson #967;2 tests, base-line logit models or log-linear models. This corresponds to assuming that the response variable is nominal and information about the ordering of the categories will be ignored. Alternatively numbers can be attached to the response categories, e.g., 1,2, . . . , J and the resulting scores can be analyzed by conventional linear regression and ANOVA models. This approach is in a sense over-confident since the data are assumed to contain more information than they actually do. Observations on an ordinal scale are classified in ordered categories, but the distance between the categories is generally unknown. By using linear models the choice of scoring impose assumptions about the distance between the response categories. Further, standard errors and tests from linear models rest on the assumption that the response, conditional on the explanatory variables, is normally distributed (equivalently the residuals
are assumed to be normally distributed). This cannot be the case since the scores are discrete and responses beyond the end categories are not possible. If there are many responses in the end categories, there will most likely be variance heterogeneity to which F and t tests can be rather sensitive. If there are many response categories and the response does not pile up in the end categories, we may expect tests from linear models to be accurate enough, but any bias and optimism is hard to quantify
Ti lascio con queste riflessioni... :D e ci ripenso magari stasera.
Nel frattempo se uno dei nostri cari statistici facesse un giro da queste parti...
Sì è una variabile ordinale, non mi interessa l'ordinabilità del processo, però è anche vero che i dati sono sequenziali cioè per passare da 8 a 10 è necessario passare anche per 9 e quindi il 9 è presente anche se in realtà non è voluto. Non sò se questa cosa possa cambiare un po' le cose. Intanto provo a fare l'analisi trattando A come fattori e vediamo che salta fuori. Grazie mille.
|
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 27 marzo 2014 : 10:40:09 Inserito il - 27 marzo 2014 : 10:40:09




|
Citazione:
Allora ho indicato nell'istogramma il numero di volte un certo dato si presenta, quindi per me lo 0 è un dato che è mancante. Dovrei quindi eliminare quei valori?
In generale 0 vuol dire che B non assume mai quel valore (es. per a=10 b non è mai tra 0 e 322). Se invece tu non avessi mai misurato B per a=9 dovresti indicarlo con NA (not available), per dire che B potrebbe essere in quel range, ma tu non hai dati per dirlo o meno. Ha senso? |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 28 marzo 2014 : 08:13:59 Inserito il - 28 marzo 2014 : 08:13:59




|
Citazione:
Messaggio inserito da chick80
Citazione:
Allora ho indicato nell'istogramma il numero di volte un certo dato si presenta, quindi per me lo 0 è un dato che è mancante. Dovrei quindi eliminare quei valori?
In generale 0 vuol dire che B non assume mai quel valore (es. per a=10 b non è mai tra 0 e 322). Se invece tu non avessi mai misurato B per a=9 dovresti indicarlo con NA (not available), per dire che B potrebbe essere in quel range, ma tu non hai dati per dirlo o meno. Ha senso?
Ok allora B può assumere 9, solo che io non l'ho misurato, ma se facessi un'altra misura è probabile che misuri quel valore. Quindi mi sembra di capire che dargli zero all'assenza è corretto. |
 |
|
|
chick80
Moderatore
    

Città: Edinburgh

11491 Messaggi |
 Inserito il - 28 marzo 2014 : 21:40:00 Inserito il - 28 marzo 2014 : 21:40:00




|
No, aspetta, mi sa che ci stiamo confondendo.
Quello che dico io è:
1) metti A=1 e misuri B. Ottieni 100, 300 e 500
2) metti A=2 e misuri B. Ottieni 200, 400 e 600
3) metti A=4 e misuri B. Ottieni 500, 800 e 1000
Per semplicità ipotizzo che le classi di B siano 0-99, 100-199, 200-299, ...
Quindi per A=1 avrai 0 misure in 0-99, 1 in 100-199, 0 in 200-299, e così via
Per A=2 avrai 0, 0, 1, 0, 1,...
Per A=3 non avrai tutti 0, perchè quei valori non li hai mai misurati! Quindi o non consideri 3 nella tua analisi oppure lo indichi come NA (ma se ti mancano tutti i valori è come non considerarlo). |
Sei un nuovo arrivato?
Leggi il regolamento del forum e presentati qui
My photo portfolio (now on G+!) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 30 marzo 2014 : 16:24:50 Inserito il - 30 marzo 2014 : 16:24:50




|
Citazione:
Messaggio inserito da chick80
No, aspetta, mi sa che ci stiamo confondendo.
Quello che dico io è:
1) metti A=1 e misuri B. Ottieni 100, 300 e 500
2) metti A=2 e misuri B. Ottieni 200, 400 e 600
3) metti A=4 e misuri B. Ottieni 500, 800 e 1000
Per semplicità ipotizzo che le classi di B siano 0-99, 100-199, 200-299, ...
Quindi per A=1 avrai 0 misure in 0-99, 1 in 100-199, 0 in 200-299, e così via
Per A=2 avrai 0, 0, 1, 0, 1,...
Per A=3 non avrai tutti 0, perchè quei valori non li hai mai misurati! Quindi o non consideri 3 nella tua analisi oppure lo indichi come NA (ma se ti mancano tutti i valori è come non considerarlo).
Non ci siamo confusi :) |
 |
|
|
serbring
Utente Junior


486 Messaggi |
 Inserito il - 09 aprile 2014 : 08:07:23 Inserito il - 09 aprile 2014 : 08:07:23




|
Ciao a tutti,
sto analizzando questi dati. Attualmente per cercare di semplificare il problema sto cercando di analizzare i dati univariati. Nello specifico per ciascuna matrice fissat un certo valore di A si calcola una grandezza denominata D che è pari a: D=sum(MeanBinB^4*H/100000)
MeanBinB è il valore medio di ciascuno intervallo. Quindi a titolo di esempio per A=5 ho il seguente istogramma
bin_B
0 - 322 632
322 - 644 138
644 - 966 364
966 - 1288 400
1288 - 1611 74
1611 - 1933 14
1933 - 2255 12
2255 - 2577 0
2577 - 2900 0
>2900 0
e quindi facendo D(5)=161^4*632+483^4*138+....
Ho diverse matrici identiche a quelle che sono le diverse ripetizioni del fenomeno e mi servirebbe stimare la distribuzione di D(5), D(6), D(7) e così via e poi calcolarne per ciascuno di esso il 95° percentile.
Ho provato a stimare una distribuzione solamente che in alcune ripetizioni ho tutti zeri per un determinato D(BinA). Questo mi da dei grattacapi nel calcolo della distribuzione ottimale, ad esempio la weibull che quella che mi da i risultati migliori mi da questo risultato:
http://s29.postimg.org/e6yl3l2rr/weibull_plot_bad.jpg
Eliminando gli zeri la distribuzione fitta meglio i dati.
http://s28.postimg.org/rzm6qwin1/weibull_plot_good.jpg
E' corretto rimuovere gli zeri?
grazie
|
 |
|
| |
Discussione |
|
|
|
Quanto è utile/interessante questa discussione:
| MolecularLab.it |
© 2003-24 MolecularLab.it |
 |
|
|





